What Is Data Regression?
Regression analysis is a set of statistical methods used for the estimation of relationships between a dependent variable and one or more independent variables. It can be utilized to assess the strength of the relationship
between variables and for modeling the future relationship between them.
Regression Analysis – Linear Model Assumptions
Linear regression analysis is based on six fundamental assumptions:
- The dependent and independent variables show a linear relationship between the slope and the intercept.
- The independent variable is not random.
- The value of the residual (error) is zero.
- The value of the residual (error) is constant across all observations.
- The value of the residual (error) is not correlated across all observations.
- The residual (error) values follow the normal distribution.
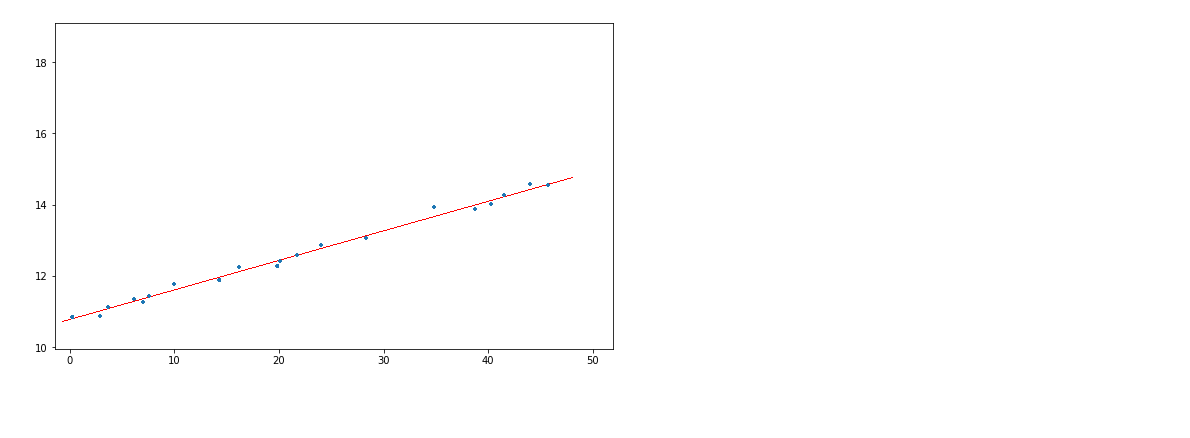
Regression Analysis – Simple Linear Regression
Simple linear regression is a model that assesses the relationship between a dependent variable and an independent variable. The simple linear model is expressed using the following equation:
Y = a + bX
- Y – Dependent variable
- X – Independent (explanatory) variable
- a – Intercept
- b – Slope
Regression Analysis – Multiple Linear Regression
Multiple linear regression analysis is essentially similar to the simple linear model, with the exception that multiple independent variables are used in the model. The mathematical representation of multiple linear regression is:
Y = a + bX1 + cX2 + dX3
- Y – Dependent variable
- X1, X2, X3 – Independent (explanatory) variables
- a – Intercept
- b, c, d – Slopes

Multiple linear regression follows the same conditions as the simple linear model. However, since there are several independent variables in multiple linear analysis, there is another mandatory condition for the model:
Non-collinearity: Independent variables should show a minimum correlation with each other. If the independent variables are highly correlated with each other, it will be difficult to assess the true relationships between the dependent and independent variables.
Regression Analysis – Logistic Regression
Logistic regression is used to analysis when only two outcomes are possible, 'Yes' & 'No'; 'Bought' & 'Did not buy', 'Pass' & 'Fail' ...
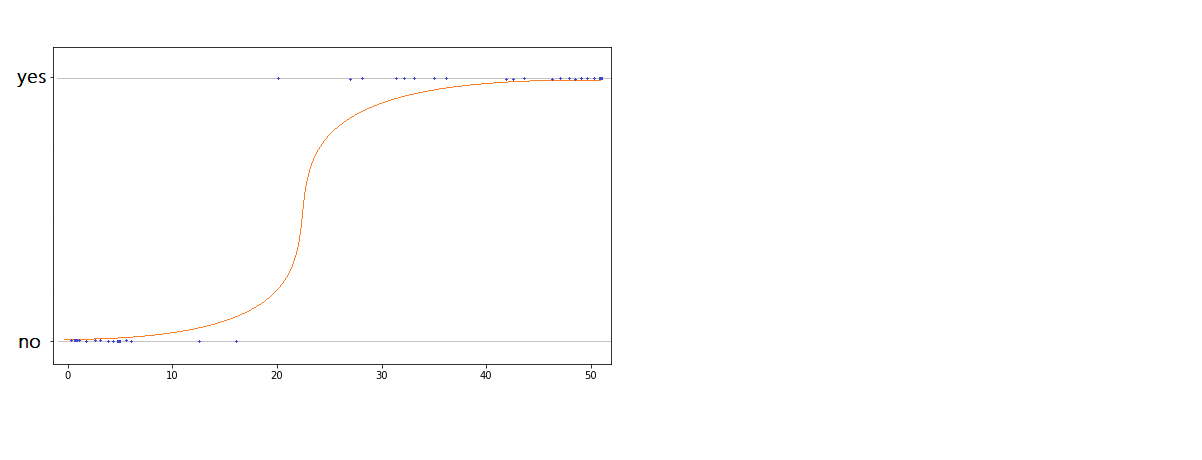
ASSUMPTIONS:
- The dependent variable is binary.
- There should be no, or very little, multicollinearity between the predictor variables.
- Logistic regression requires fairly large sample sizes.





