Do two social platforms generate the same response to the ad?
EXAMPLE:
Company X was running an online campaign on two social platforms. After some period of time,
company decided to check if advertisement has the same response (similar amount of clicks) on different platforms.
Samples for two platforms were taken at random days over the same time period.
I placed two platform samples into a SPSS. First platform has assigned value of 1 and the second = 2, and started to perform means comparison for independent samples
(two different platforms are not depending on each other).
Company is looking for a difference between platforms.
A two sample t-test is used to test whether or not the means of two populations are equal.
Test is used when all below statements are TRUE:
- 1. Want to compare scores of two groups (not more than 2).
- 2. Groups are independent.
- 3. Samples have normal distribution.
- 4. Sample size is small ( < 30).
- H0: there is no difference between platforms
- H1: there is a difference between platforms
- Significance level of alpha = .05
- Sample size : n = 12
I will accept H0 if Sig > alpha and reject H0 if Sig < alpha.
RESULTS:
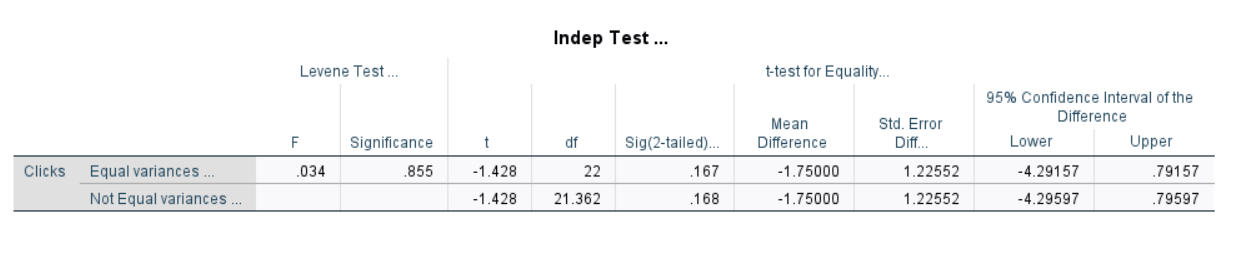
The table displays the results of the two sample t-test. The first row shows the results
of the test if I assume that the variance between the two groups is equal. The second row shows
the results of the test without this assumption.
In this case, the two versions of the test produce nearly identical results.
- t: The test statistic, found to be -1.428
- df: The degrees of freedom, calculated as n1+n2-2 = 12+12-2 = 22
- Sig. (2-tailed): The two-sided p-value that corresponds to a t value of -1.428 with df=22
INTERPRETATION:
Since the p-value of the test (.167) is not less than 0.05, I fail to reject the null hypothesis.
I do not have enough evidence to say that the means between platforms are different.
Both platforms brings the same respond to the advertisement.




